-  Grad 7 / 1.1: Pythagoras sats: hitta längden på hypotenusan

1. 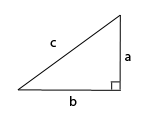     I den rätvinklig triangel ovan, om a = 3 och b = 4, vad är längden på hypotenusan c? 4             5             6

2. 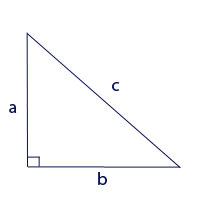     I den rätvinklig triangel ovan, om a = 9 och b = 12, vad är längden på hypotenusan c? 15             16             18

3. 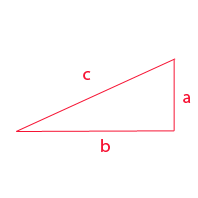     I den rätvinklig triangel ovan, om a = 5 och b = 12, vad är längden på hypotenusan c? 15             14             13

4.      I den rätvinklig triangel ovan, om a = 6 och b = 8, vad är längden på hypotenusan c? 9             10             11

5.      I den rätvinklig triangel ovan, om a = 15 och b = 20, vad är längden på hypotenusan c? 23             24             25

6.      I den rätvinklig triangel ovan, om a = 10 och b = 24, vad är längden på hypotenusan c? 25             26             27

7.      I den rätvinklig triangel ovan, om a = 12 och b = 16, vad är längden på hypotenusan c? 18             19             20

8.      I den rätvinklig triangel ovan, om a = 21 och b = 28, vad är längden på hypotenusan c? 35             36             37

9.      I den rätvinklig triangel ovan, om a = 15 och b = 36, vad är längden på hypotenusan c? 37             38             39

10.      I den rätvinklig triangel ovan, om a = 18 och b = 24, vad är längden på hypotenusan c? 29             30             31

© 2011 Tao Math Learning. All rights reserved.